Killer Sudoku Tips and Strategies

Killer Sudoku Solving Strategies

There are three basic methods used to solving killer sudoku puzzles. The first is to use the strategies for solving regular sudoku puzzles. The second is to consider the different ways that a sum can be created. The third is to consider the total value of a region. Here we outline the basic strategies and then show how they are applied in a sample puzzle. At a later date we will post more complex strategies. (The Terminology used on this page is defined on the rules page.)

Basic Solving Strategies

The following are the basic rules used to solve killer sudokus.

Rule of 1: This comes directly from the definition of sudoku. No region can contain any duplicate digits. In a sudoku region each digit appears exactly once. For example, if a digit appears in a row, it cannot be in any other cell in the row. Likewise, each digit can appear in a cage only once. If a digit is in a cage, it cannot appear in that cage again.
Rule of Necessity: This rule can be applied to sudoku regions (i.e., row, column, or nonet) or to a cage. In the former case, each region must contain all the digits one to nine. Thus, if all the digits but one appear in a row, the missing digit must appear in the empty cell.
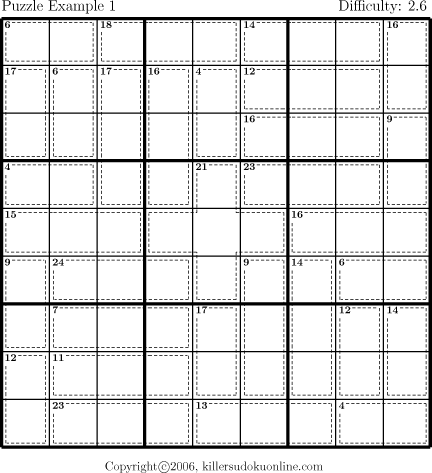
Rule of 45: Each sudoku region (i.e., row, column, or nonet) contains the digits one through nine. Thus, each sudoku region has a total value of 45. If S is the sum of all the cages contained entirely in a region, then the cells not covered must sum to 45-S.
Rule of K: The Rule-of-k is an extension of the Rule-of-1. If there are k cells contained entirely in a region that contain exactly k different possible values, then no other cell in that region can contain any of those k values.
Sum Elimination

more to come...

Applying the basic strategies. An Example

Here we will use the above strategies to solve a puzzle. You might want to print out the puzzle so you can follow along all the steps.

Rule of 45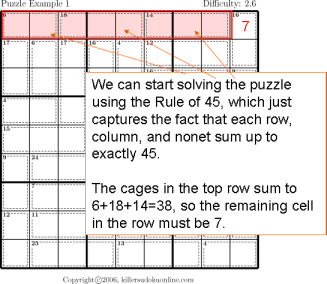

Rule of necessity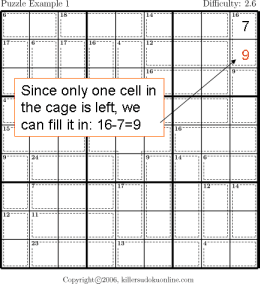

Rule of 1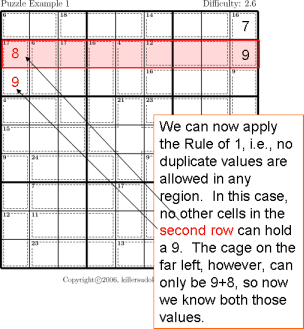

Unique Sums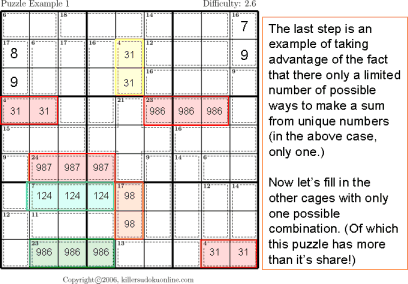

Rule of K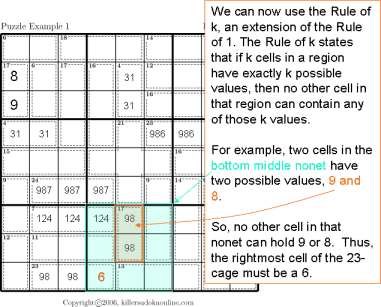

Rule of K
Limited possible sums

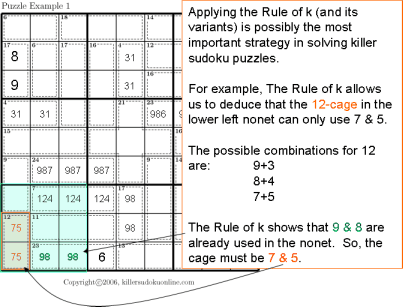Rule of necessity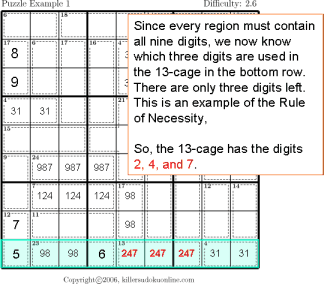

Limited Possible Sums

Rule of K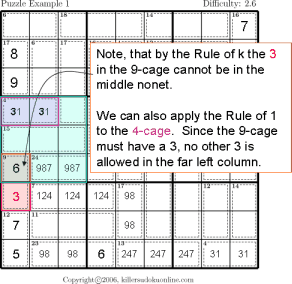

Limited Possible Sums
Rule of 1
Rule of K

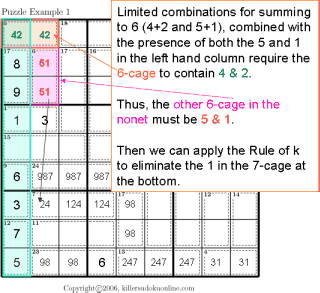Rule of Necessity
Rule of 1
All Possible Sums

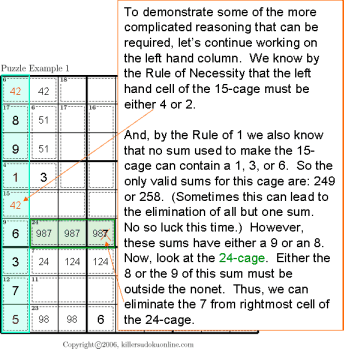Rule of Necessity
Limited possible sums

Rule of K
Rule of 1
Limited Possible Sums

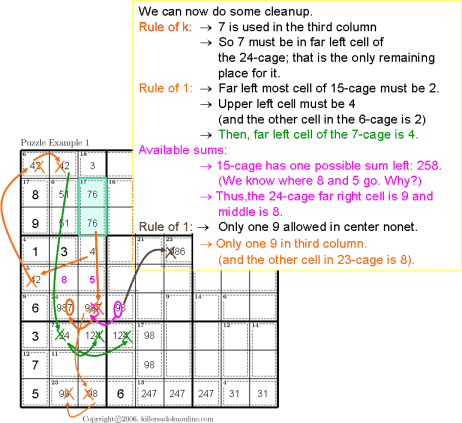Remaining sum
Rule of 1
Rule of K
Rule of necessity

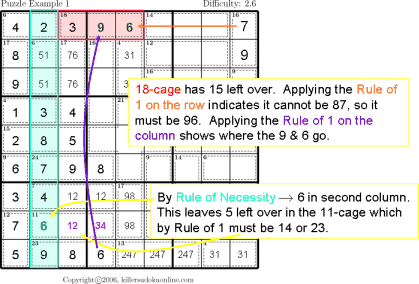Sum Elimination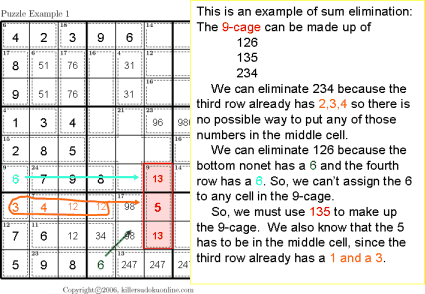

Sum elimination
Rule of 1

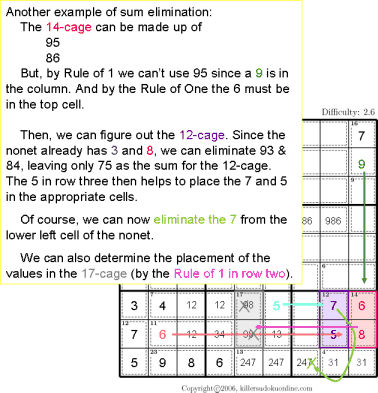Range of Totals
Sum Elimination

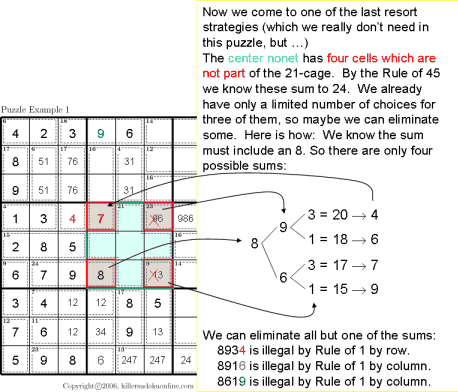Rule of 1
Rule of necessity
Remaining Sum

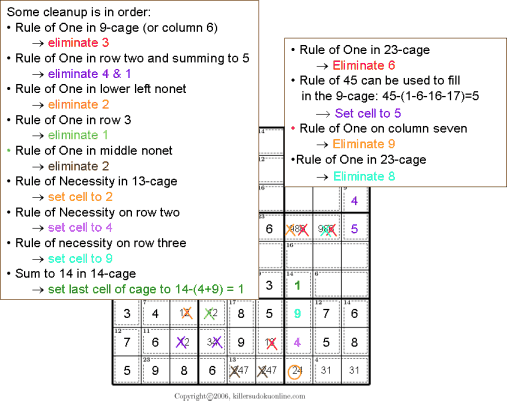Limited possible sums
Rule of 1
Rule of necessity

Rule of necessity
Rule of 1

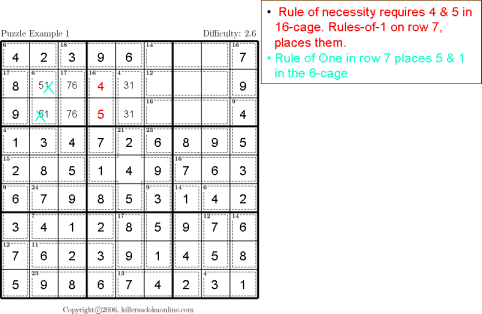Vote for our site

Thank-you!

iPhone Features?

Table of Contents

Killer Sudoku Solving Strategies

Basic Solving Strategies

Applying the basic strategies. An Example