Approach to Weekly No. 28
Here is an approach to Weekly No. 28.
|
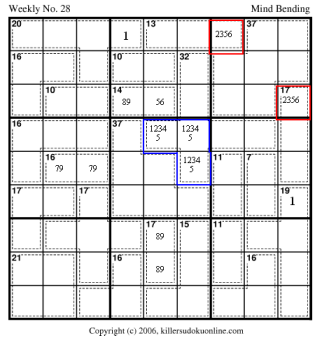
Use the rule of 45 to determine the values of R9C4 and R4C9.
Use the rule of 45 combined with the ones in R1 and C9 to fill in the red-region in the upper right nonet. Use the rule of 45 to fill in the blue region in the center nonet. There is only one possible sum for the 17-cage in C5 and the 16-cage in R5. The 17-cage limits the possible values in the 14-cage on R7. |
 |
|||||||||||||||||||||||||||||||||||||||
|
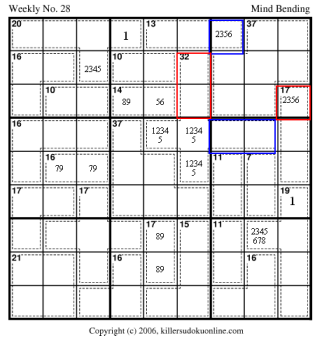
The rule of 45 determines that the red region must be 15.
Use the rule of 45 on R89 (using the red region value of 15) to determine the value of R9C89-R8C3=12. Since the maximum value of R9C89 is 17, the maximum value of R8C3 is 5. Since there is already a 1 in the 20-cage, the possible values of R8C3 are 2345. And the possible range of values for R9C89 is 14 to 17. Likewise, the blue region is 17 and the value of R89C9-R3C8=9. Thus, the possible range of values for R89C9 is 11 to 17. And, the possible values for R3C8 is 2345678.
|
 |
|||||||||||||||||||||||||||||||||||||||
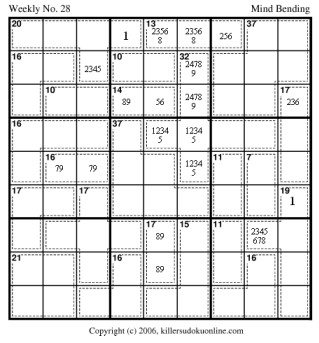
The parts of the 13-cage and 32-cage in the middle top nonet must sum to 20.
We can eliminate: 65 from R9C56 as it makes the 14-cage impossible We can eliminate 85 from R78C6 for the same reason
We can eliminate 34 from R9C56 as it makes the 32-cage impossible. We can elimainte 93 and 75 from R78C6 as it makes the 14-cage impossible.
Now look at R7C9. If R9C56 sums to 10, R9C7 will be 3 and then, R7C9 would be 5. This requires an 86 in the 14-cage. This eliminates 28,46 from R9C56 and 82,64 from R78C6. Leaving only 73 for both. so, R9C56 cannot sum to 10. Likewise, if R9C56 sums to 11, R7C9 would be 6, requiring 95 in the 14-cage. Thus, the possible sums are:
|
 |
|||||||||||||||||||||||||||||||||||||||
|
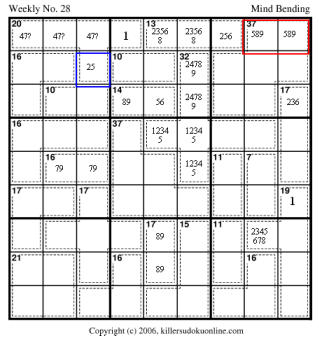
Look at the 13-cage: It is either 256 or 238. This means that
all the sums for the 20-cage that contain 2 and (5 or 6) and (3 or 8)
are illegal. This leaves: 12467 or 13457.
This means a 7 must be in R9C123. This means the possible sums for the red region, R9C89 are: 86,95,96,98. Since 16 is no longer legal, R8C3 cannot be a 4. Thus, 4 and 7 must be in R9C123. If 12467 is the sum, then R8C3 will be 2. Making the 13-cage 382. Making the red region 95. If 13457 is the sum, then R8C3 will be 3 or 5. 3 -> 13-cage is 382 and red-region is 96 which would be illegal (due to R6C9). 5 -> 13-cage is 256 and red-region is 983
|
 |
|||||||||||||||||||||||||||||||||||||||
|
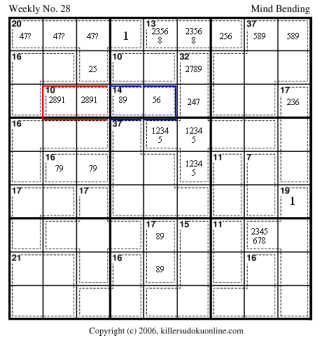
Now look at the 10-cage at R7C23 (in red). It is either 19 or
28 (because of the values used in the 20-cage).
So, the 10-cage contains either 8 or 9. And on the same row the 14-cage (in blue) uses either 8 or 9. So, no other uses of 8 or 9 are legal on R7. Thus, R7C6 cannot contain 8 or 9 and R8C6 cannot contain a 4.
|
 |
|||||||||||||||||||||||||||||||||||||||
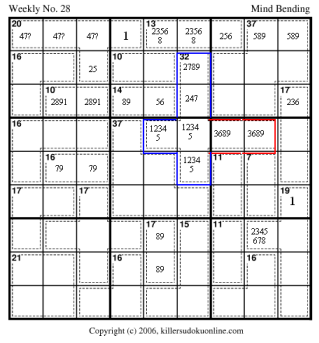
Now lets return to the 32-cage.
We know the possible sums for R6C78 (in red) are: 32-8-(9 or 12 or
13)=15,12,11. Furthermore, the values used to make the sums in the blue
part of the 32-cage limit the possible values in the red region:
|
 |
|||||||||||||||||||||||||||||||||||||||
|
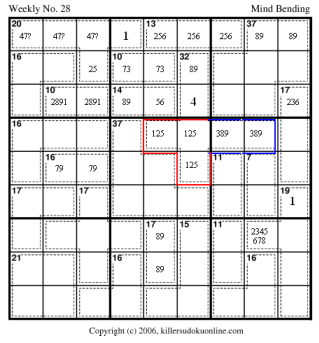
Now
we can eliminate the possibility of 832 as a possible sum for the
13-cage on R9. 832 is only possible if the 14-cage is 95. However, a 95
in the 14-cage requires an 82 in the 10-cage at R7C23; which makes R8C3
a 5 giving the 20-cage a 3 in R9; which conflicts with the 13-cage also
in R9. So, the 13-cage must be 265. Therefore, R9C89 must be 98.
This eliminates the 27 as a possibility in R78C6. Which also sets the red region to 125. And eliminates the 6 from the blue region. It also gives us 73 for the 10-cage at R8C45. |
 |
|||||||||||||||||||||||||||||||||||||||
|
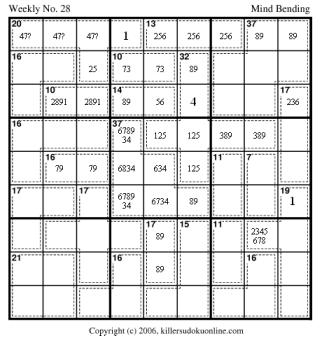
The next step is to fill in the 37-cage with the values we know it must have: 346789.
|
 |
|||||||||||||||||||||||||||||||||||||||
|
The red and blue region must both have 3 and 7. Therefore, 3 and 7 must both be in R123C6. There is only one possible sum to 15 that includes 1, 3, and 7. This leaves 256 for the leftmost column of the nonet.
|
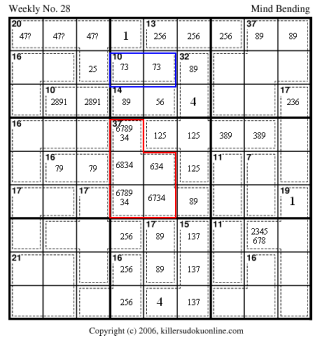 |
|||||||||||||||||||||||||||||||||||||||
|
Now we can do a lot of clean up.
The rest of the puzzle should fall into place. |
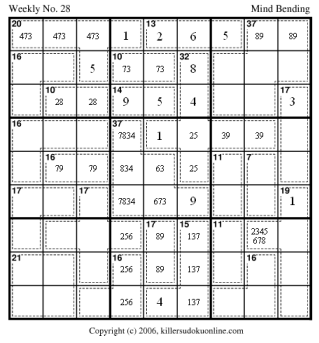 |









